 |
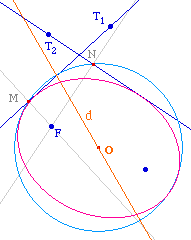
On sait que la projection orthogonle du foyer d'une conique bifocale sur une de ses tangentes appartient au cercle principal de cette conique, dont le centre est aussi celui de la conique.Soient alors M et N les projections orthogonales de F sur les tangentes T1 et T2 respectivement. Le centre O de la conique appartient à la droite d, médiatrice de [MN]. On peut alors construire la conique : en prenant un point sur objet O de cette droite, on construit le second foyer, et on utilise la macro proposée en introduction.
|
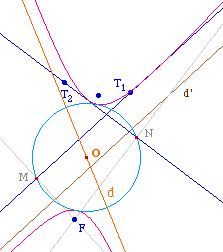 |
La conique est une ellipse si et seulement si les foyers sont à l'intérieur du cercle principal (de centre O passant par M ou N) donc si et seulement si OF < OM, soit ssi O est plus prés de M que de F.Ainsi, sur le lieu de O - médiatrice d de [MN] - on distingue, en général, deux demi-droites construites à partir del'intersection de cette droite d avec la médiatrice d' de [MF].Si O et F sont d'un même côté de d', la conique est une ellipse, sinon c'est une hyperbole. O sur la médiatrice de [MF] aboutit à une conique dégénérée. |
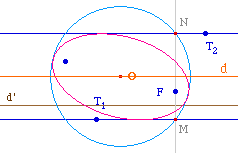 |
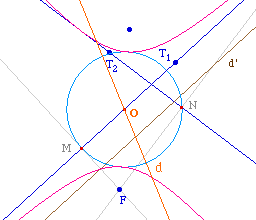
On remarquera que si les deux tangentes T1 et T2 sont parallèles, les droites d et d' sont elles aussi parallèles, il n'y a donc qu'un seul type de conique quelque soit la position du point O sur la médiatrice de [MN].C'est une ellipse pour F entre les deux tangentes, une hyperbole sinon (voir ci-dessous).
|
 |
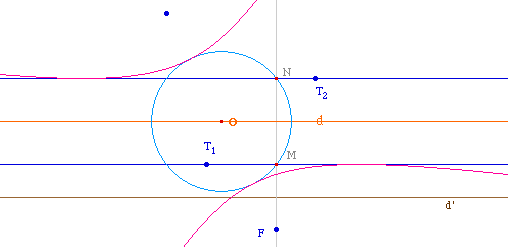
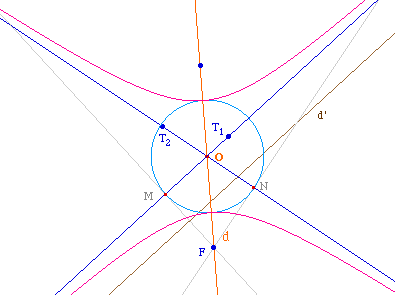
Comme dans d'autres situations avec les hyperboles, certaines conditions s'accommodent bien d'un passage à l'infini. Ainsi, si O est sur l'une des tangentes, la construction continue d'exister (y compris avec Cabri en redéfinissant le point O comme intersection de deux droites), et ladite tangente devient alors tangente à l'infini, c'est-à-dire asymtote.Remarque : On a en fait ici la construction d'une hyperbole par foyer, tangente et asymptote. |
|
|