|
|
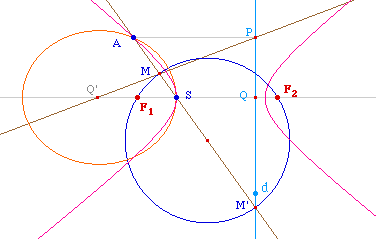
Au lieu du centre, on se donne le sommet, et donc
à nouveau l'axe focal, avec cette fois, la même
démarche que pour la première construction du
cas général pour construire le premier cercle
lieu du foyer puisque l'on a deux points de la conique.
La démarche est la même que ci-dessus. Il
est clair qu'il y a en général deux solutions
car cette fois le cercle de diamètre [MM']
coupe toujours l'axe focal, sauf le cas trivial où A
serait sur cet axe : il n'existe alors pas de conique dans
ce cas. Selon la position de A, S et d, on obtient deux
coniques de même type ou de types différents
comme illustré ci-dessus.
 La macro CnkDirSA.mac
correspondante.
La macro CnkDirSA.mac
correspondante.
|