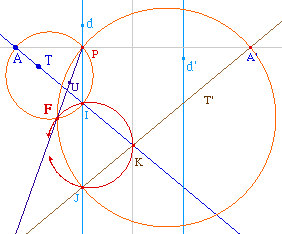|
|
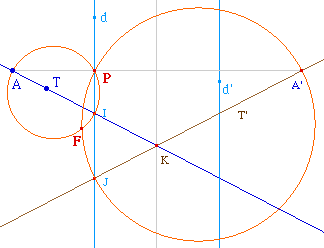
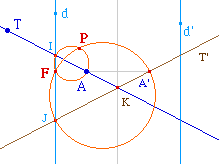
On note alors naturellement F ce foyer et P le point
d'intersection des deux cercles qui est sur la
directrice.
Si on fait le lieu de F, il est vite clair que le
segment [IJ] obtenu correspond à une question
d'orientation de l'intersection des cercles quand A passe
entre les deux droites.
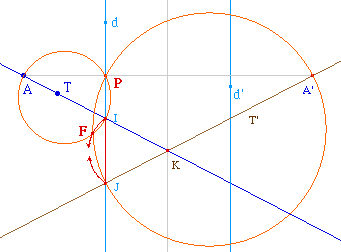
Pour s'en convaincre, on peut effectuer le lieu de P au
lieu de F, dans la même configuration :
|
|
|
On trouve l'autre arc d'un cercle et l'extérieur
du segment [IJ].
Il semble clair que le lieu de F est le cercle
circonscrit au triangle IJK - Quand celui-ci existe - mais
il serait intéressant de pouvoir construire ce lieu
correctement, c'est - à dire de pouvoir construire
effectivement le point F comme étant l'autre
intersection des deux cercles que celle sur la directrice
d.
C'est ce que nous allons détailler dans la
suite.
|
|
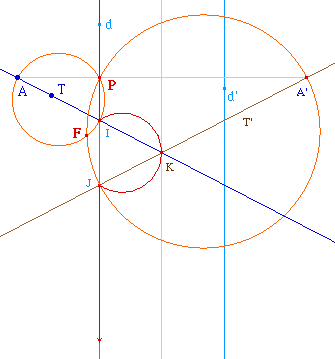
On voit ici clairement l'inverion des points P et F
entre le cas où A est extérieur à la
bande des deux directrices (hyperbole) et le cas où A
est intérieur à cette bande.
|