|
|
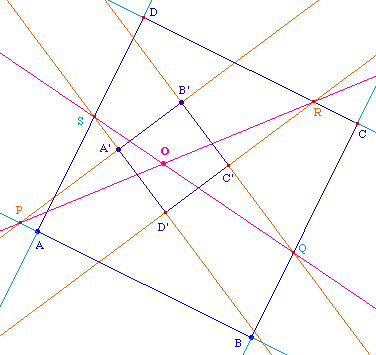
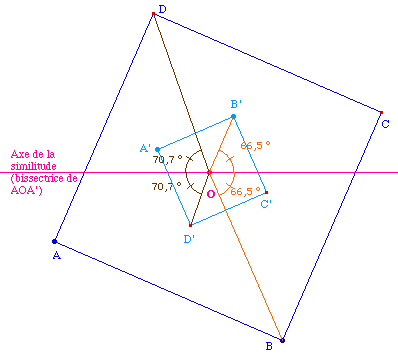
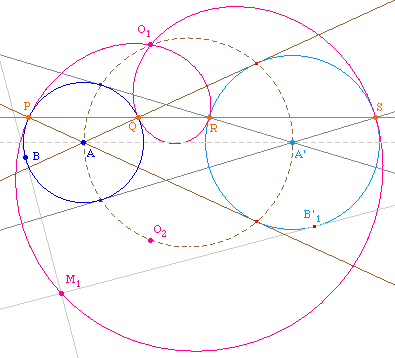
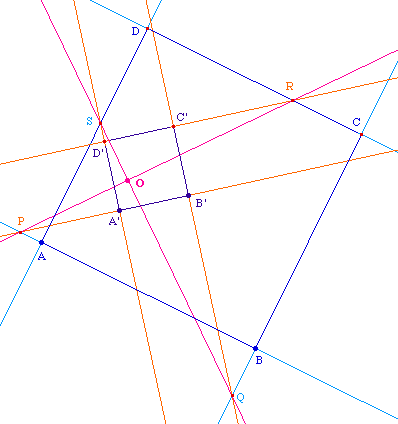
Construisons un carré ABCD sur le segment
[AB] et un carré A'B'C'D' de même sens
sur le segment [A'B']. Notons P, Q, R, S les points
d'intersection respectifs des côtés homologues
des deux carrés, à savoir (AB) et (A'B'), (BC)
et (B'C'), (CD) et (C'D'), (DA) et (D'A'). Appelons P' et R'
les images - non construites sur la figure - de P et R par s
(images qui se trouvent respectivement sur les droites
(A'B') et (C'D')), O le point d'intersection des droites
(PR) et (P'R'), et O' l'image de O par s.
D'après le théorème de
Thalès, on a 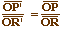 .
D'autre part, s étant une application affine, elle
conserve les rapports de mesures algébriques; en
particulier, .
D'autre part, s étant une application affine, elle
conserve les rapports de mesures algébriques; en
particulier, 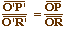 .
Finalement on a .
Finalement on a 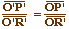 ,
ce qui prouve que O' = O, ou encore que O est le centre
cherché. L'important est de remarquer que O se trouve
sur la droite (PR). Par le même raisonnement, il se
trouve aussi sur la droite (QS), ce qui permet d'achever la
construction : O est l'intersection des droites (PR) et
(QS). ,
ce qui prouve que O' = O, ou encore que O est le centre
cherché. L'important est de remarquer que O se trouve
sur la droite (PR). Par le même raisonnement, il se
trouve aussi sur la droite (QS), ce qui permet d'achever la
construction : O est l'intersection des droites (PR) et
(QS).
|