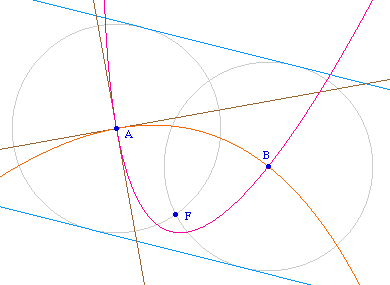
|
|
Si le triangle AFB est isocèle en F, les deux
cercles passant par F ont même rayon, et, s'ils ont
encore des tangentes communes extérieures, ils n'ont
plus de centre d'homothétie de rapport positif. La
construction précédente résiste
à cette situation (ci-dessous B est sur objet d'un
cercle).
La figure PBSol01b.fig
de ce cas particulier.
On remarquera que les tangentes en
l'un des points A ou B sont orthogonales. C'est une
propriété classique des paraboles homofocales
: même foyer et même axe, ce qui est le cas ici.
La preuve de ce résultat est immédiate, nous y
reviendrons néanmoins à l'item Exercices (D)
dans un cas un peu plus général que cette
situation.
|
